Spatial domain, Frequency domain, Time domain and Temporal domain..

Hi all,

This post will describe what is Spatial Domain, Frequency Domain, Time Domain and Temporal Domain.

Brief idea

1. Spatial Domain (Image Enhancement)

Kernel Operator / Filter mask

Definition

• is manipulating or changing an image representing an object in space to enhance the image for a given application.
• Techniques are based on direct manipulation of pixels in an image
• Used for filtering basics, smoothing filters, sharpening filters, unsharp masking and laplacian

Techniques

• Smoothing

Smoothing Operator

Averaging Mask

• Unsharp Masking
• Image manipulation technique for increasing the apparent sharpness of photographic images. 
• this technique uses a blurred or unsharp, positive to create a mask of the original image. 

Unsharp Mask Example

• Laplician
• Highlight regions of rapid intensity change and is therefore often used for edge detection.
• often applied to an image that has first been smoothed with something approxiating in order to reduce  its sensitivity to noise.

Edge Detection Operator

Edge Detection Example

Reference : http://www.ee.columbia.edu/~xlx/ee4830/notes/lec4.pdf

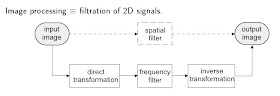
2. Frequency Domain


Definition

• Techniques are based on modifying the spectral transform of an image
• Transform the image to its frequency representation
• Perform image processing
• Compute inverse transform back to the spatial domain
• High frequencies correspond to pixel values that change rapidly across the image (e.g. text, texture, leaves, etc.)
• Strong low frequency components correspond to large scale features in the image (e.g. a single, homogenous object that dominates the image) 

Technique

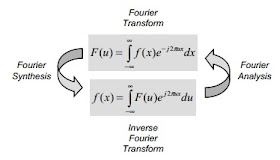
• Fourier Transform
• Function that are not periodic but with finite area under the curve can be expressed as he integral of sines and/ or sines multiplied by a weight function

• Filtering example : Smooth an image with a Gaussian Kernel 
• Procedure:  

Image convolve with Gaussian Kernel

Result of Filtered Image

Reference : http://www.cse.lehigh.edu/~spletzer/rip_f06/lectures/lec012_Frequency.pdf




3. Time Domain

To explain about the time domain, we would like to compare it with frequency domain.

• The time domain (or spatial domain for image processing) and the frequency domain are both continuous, infinite domains. There is no explicit or implied periodicity in either domain. This is the what we call the Fourier transform.
• The time domain is continuous and the time-domain functions are periodic. The frequency domain is discrete. We call this the Fourier series.
• The time domain is discrete and infinite, and the frequency domain is continuous. In the frequency domain the transform is periodic. This is the discrete-time Fourier transform (DTFT).
• The time domain and the frequency domain are both discrete and finite. Although finite, the time and frequency domains are both implicitly periodic. This form is the discrete Fourier transform (DFT).

Reference : http://blogs.mathworks.com/steve/2009/11/23/fourier-transforms/

Temporal Domain


Temporality is described here as the ratios of, or relative intervals between events. The temporal domains carries no information about frequency or sequence. One way to represent the temporal domain from the time-line is as below:

We can use a variety of natational conventions, and to construct this notation, we counted the time intervals starting with the interval of the first event (Q) up to the interval just before the second event (G) which equaled 10 intervals. We will continued with similar fashion for each of the other events. For simplicity, we can divided all numbers gleaned by five for the smallest whole number representation of the intervals. The resulting chart is represented as follow:

This chart can be simplified quite a bit further but has been left completely filled in for clarity. It not holding sequential information, however the sequence is revealed because of the way we write it. Below is the same chart of temporal information but presented without giving away any of the original sequence information.

The only information carried in the temporal domain are the distances between events relative to the distances between other events; for example "There is twice as much time between A and X as there is between G and Q". The actual intervals could be microseconds, years, or centuries among other things. The temporal representation retains no hint of this.

The measured distance between any two events could be hours in one observation and microseconds or years in the next observation. As long as the ratios of measured distances between events remain the same, the temporal domain representation will remain the same.

The arrow key example in figure below may be a little confusing. When displayed on a terminal, put the cursor on the Q and use the arrow key to move to the G. It doesn't matter if you go left the down the left, it will be the same number of key-presses as you will use in the two diagrams above it.

This shows that, just as with the frequency and sequential domains, information from the other two component domains is lost when we convert from the time domain to the temporal domain and back. Also, if we start with only temporal information we can convert back and forth between it and the time domain without any loss of the original information.

The other two component domains share a similar relationship to the time domain. The relationships between the time domain and its three component domains can be represented as below:

Lastly, each of the frequency, sequential, and temporal domains do seem to overlap with the information about the time domain contained within their two counterpart component domains.



Reference: http://standoutpublishing.com/Doc/o/Temporal/Temporal.shtml
 http://forum.videohelp.com/threads/281753-Image-Processing-Temporal-Spacial-Median-filter
http://gisknowledge.net/topic/ip_in_the_temporal_domain/trodd_temporal_domain_enhance_07.pdf